3 Forward kinematics (FK) for a planar robot manipulator
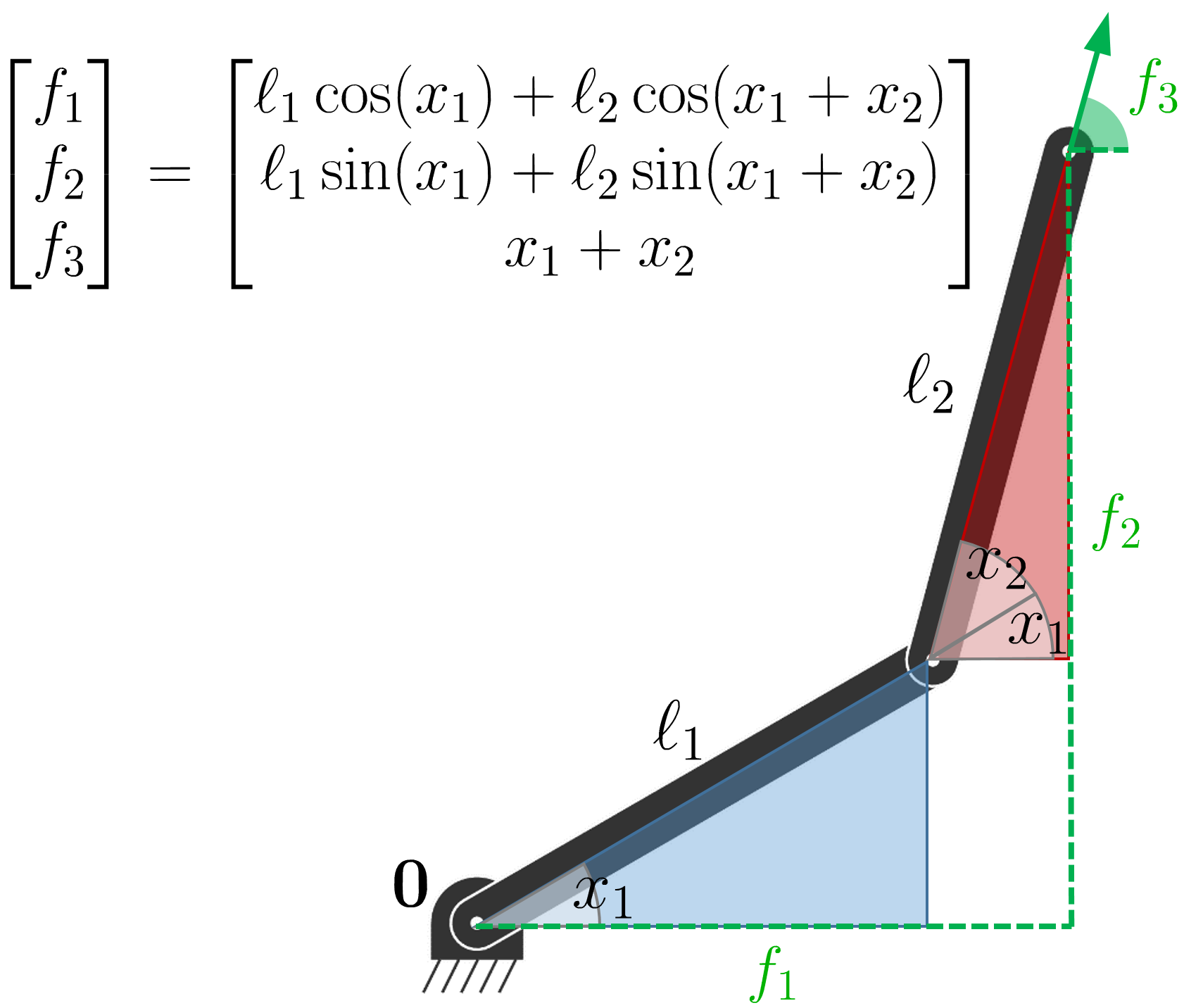
The forward kinematics (FK) function of a planar robot manipulator is defined as
| \displaystyle\bm{f} | \displaystyle=\begin{bmatrix}\textstyle\bm{\ell}^{\scriptscriptstyle\top}\cos(\bm{L}\bm{x})\\ \textstyle\bm{\ell}^{\scriptscriptstyle\top}\sin(\bm{L}\bm{x})\\ \textstyle\bm{1}^{\scriptscriptstyle\top}\bm{x}\end{bmatrix} | ||
| \displaystyle=\begin{bmatrix}\textstyle\ell_{1}\!\cos(x_{1})\!+\!\ell_{2}\!\cos(x_{1}\!+\!x_{2})\!+\!\ell_{3}\!\cos(x_{1}\!+\!x_{2}\!+\!x_{3})\!+\!\ldots\\ \textstyle\ell_{1}\sin(x_{1})\!+\!\ell_{2}\!\sin(x_{1}\!+\!x_{2})\!+\!\ell_{3}\!\sin(x_{1}\!+\!x_{2}\!+\!x_{3})\!+\!\ldots\\ \textstyle x_{1}+x_{2}+x_{3}+\ldots\end{bmatrix}\!\!, |
with \bm{x} the state of the robot (joint angles), \bm{f} the position of the robot end-effector, \bm{\ell}\, a vector of robot links lengths, \bm{L} a lower triangular matrix with unit elements, and \bm{1} a vector of unit elements, see Fig. 6 .
The position and orientation of all articulations can similarly be computed with the forward kinematics function
| \displaystyle\bm{\tilde{f}} | \displaystyle={\Big[\bm{L}\;\mathrm{diag}(\bm{\ell})\cos(\bm{L}\bm{x}),\quad\bm{L}\;\mathrm{diag}(\bm{\ell})\sin(\bm{L}\bm{x}),\quad\bm{L}\bm{x}\Big]}^{\scriptscriptstyle\top} | ||
| \displaystyle=\begin{bmatrix}\textstyle\tilde{f}_{1,1}&\tilde{f}_{1,2}&\tilde{f}_{1,3}&\ldots\\ \textstyle\tilde{f}_{2,1}&\tilde{f}_{2,2}&\tilde{f}_{2,3}&\ldots\\ \textstyle\tilde{f}_{3,1}&\tilde{f}_{3,2}&\tilde{f}_{3,3}&\ldots\\ \end{bmatrix}\!\!, |
| \displaystyle\tilde{f}_{1,1}=\ell_{1}\!\cos(x_{1}),\quad | \displaystyle\tilde{f}_{1,2}=\ell_{1}\!\cos(x_{1})\!+\!\ell_{2}\!\cos(x_{1}\!+\!x_{2}),\quad | \displaystyle\tilde{f}_{1,3}=\ell_{1}\!\cos(x_{1})\!+\!\ell_{2}\!\cos(x_{1}\!+\!x_{2})\!+\!\ell_{3}\!\cos(x_{1}\!+\!x_{2}\!+\!x_{3}), | |||
| with | \displaystyle\tilde{f}_{2,1}=\ell_{1}\sin(x_{1}), | \displaystyle\tilde{f}_{2,2}=\ell_{1}\sin(x_{1})\!+\!\ell_{2}\!\sin(x_{1}\!+\!x_{2}), | \displaystyle\tilde{f}_{2,3}=\ell_{1}\sin(x_{1})\!+\!\ell_{2}\!\sin(x_{1}\!+\!x_{2})\!+\!\ell_{3}\!\sin(x_{1}\!+\!x_{2}\!+\!x_{3}),\quad\ldots | ||
| \displaystyle\tilde{f}_{3,1}=x_{1}, | \displaystyle\tilde{f}_{3,2}=x_{1}+x_{2}, | \displaystyle\tilde{f}_{3,3}=x_{1}+x_{2}+x_{3}. |
In Python, this can be coded for the end-effector position part as